Segmentacja obrazu wykorzystuje histogram do podziału obrazu na dwie grupy, nazywane roboczo obiektami oraz tłem. O tym w jaki sposób działa histogram oraz jak go napisać można znaleźć informacje w osobnym materiale.

Każda z naszych grup (obiekty i tło) posiada własną wewnętrzną wariancję. Optymalny próg służący do podziału na te dwie grupy minimalizuje ten parametr, zwiększając jednorodność każdej grupy. Zacznijmy ok kilku podstawowych założeń i statystyk:

• Pierwszym założeniem jest dla nas \(T\) czyli nasza wartość progowania. Wszystkie pozostałe wzory wyliczane są dla jakiegoś \(T\). Głównym założeniem jest to że jest to wartość dzieląca przestrzeń naszego obrazu na dwie części \(o\) - czyli obiekty czyli wartości pikseli \(<=T\) oraz tło \(b\), gdzie wartości będą \(>T\). Zakładamy tutaj, że mamy jasne tło, a obiekty ciemniejsze. Nic nie szkodzi na przeszkodzie, żeby interpretować obie grupy odwrotnie.
• Podstawowymi parametrami będą prawdopodobieństwa A’ priori dla grup \(o\) oraz\(b\): \[P_o(T)=\sum_{i=0}^{T}P(i) \qquad P_b(T)=\sum_{i=T+1}^{255}P(i)\] \[P(i)=h(i)/N\] gdzie \(H(i)\) to histogram obrazu o \(N\) pikselach.
• Służą nam one do wyliczenia średnie i wariancji dla każdej z grup: \[\mu_o(T)=\sum_{i=0}^{T}\dfrac{iP(i)}{p_o(T)}\] \[\mu_b(T)=\sum_{i=T+1}^{255}\dfrac{iP(i)}{p_b(T)}\] \[\sigma_o^2(T)=\sum_{i=0}^{T}\dfrac{(i-\mu_o(T))^2 P(i)}{P_o(T)}\] \[\sigma_b^2(T)=\sum_{i=T+1}^{255}\dfrac{(i-\mu_b(T))^2 P(i)}{P_b(T)}\] Uwaga pamiętajcie, że jeżeli w danej grupie nie macie już żadnych wartości prawdopodobieństwo będzie wynosić \(0\), więc będą występować dzielenia przez \(0\), trzeba się przed tym jakoś zabezpieczyć.
• Ostatni krok to wyliczenie naszej wariancji wewnątrz grupowej: \[\sigma_W^2(T)=\sigma_o^2(T)P_o(T)+\sigma_b^2(T)P_b(T)\]

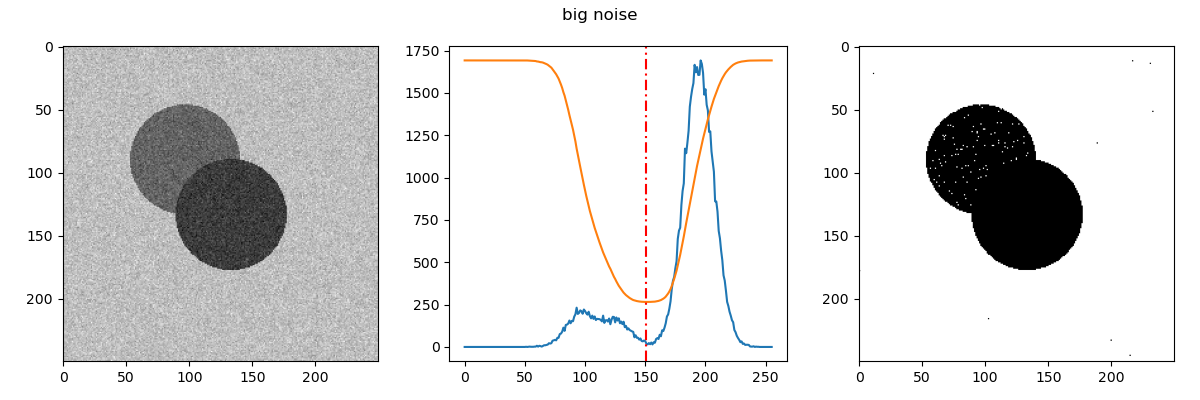
Optymalny podział można otrzymać poprzez znalezienie najmniejszej \(\sigma_W^2(T)\), co zaprezentowano na poniższym przykładzie: