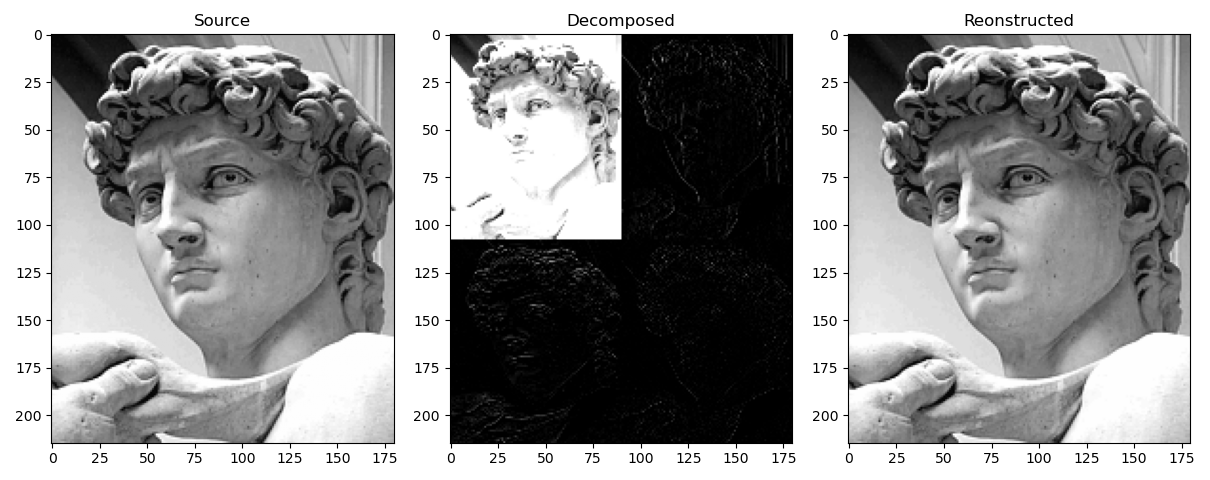
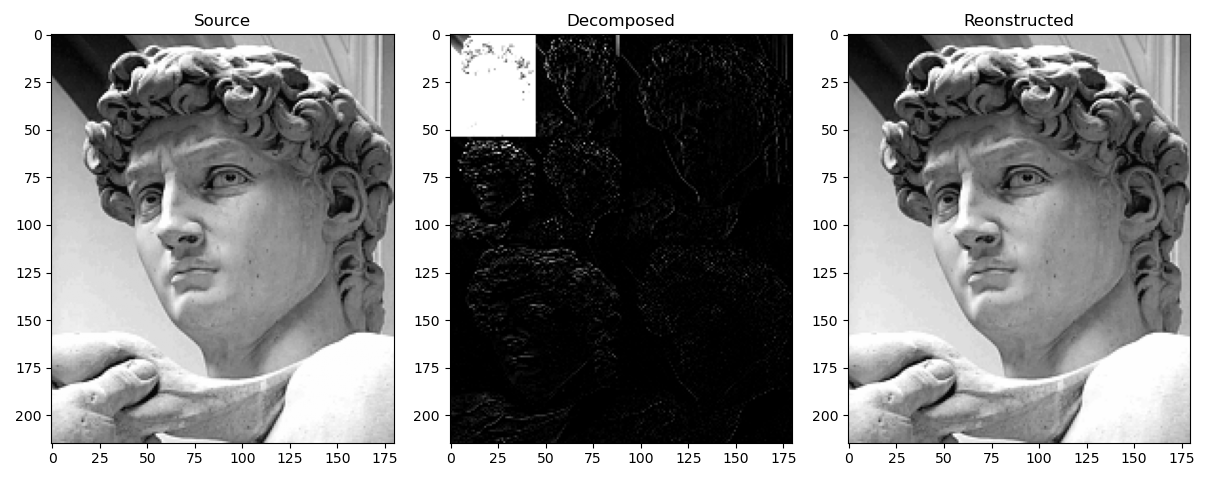
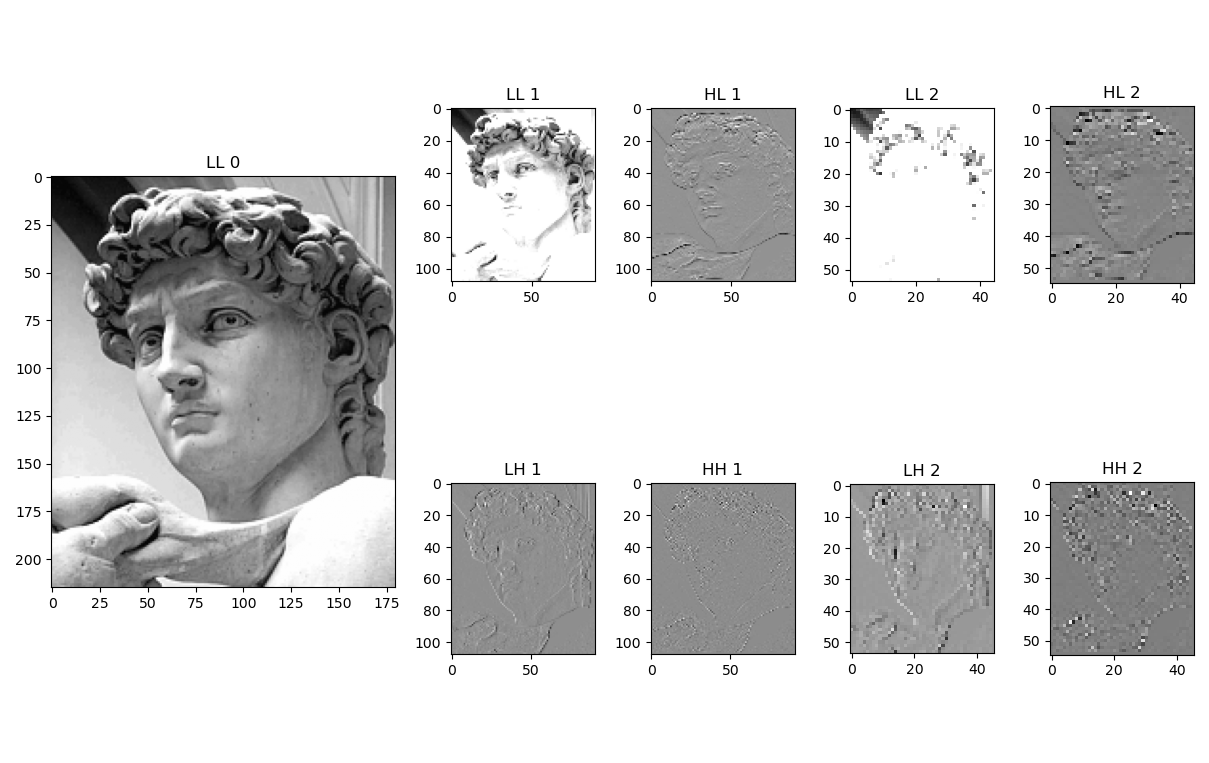
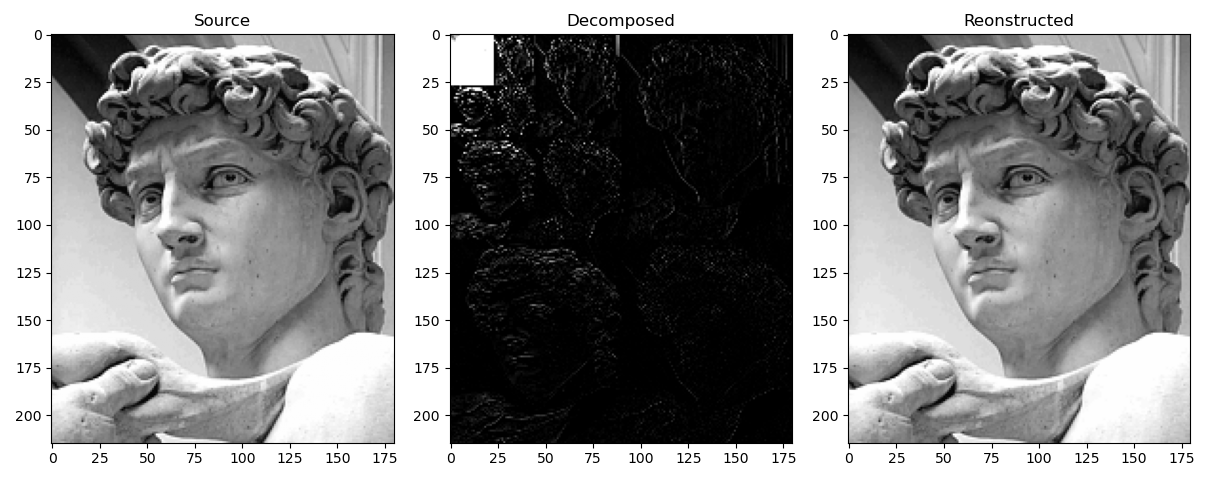
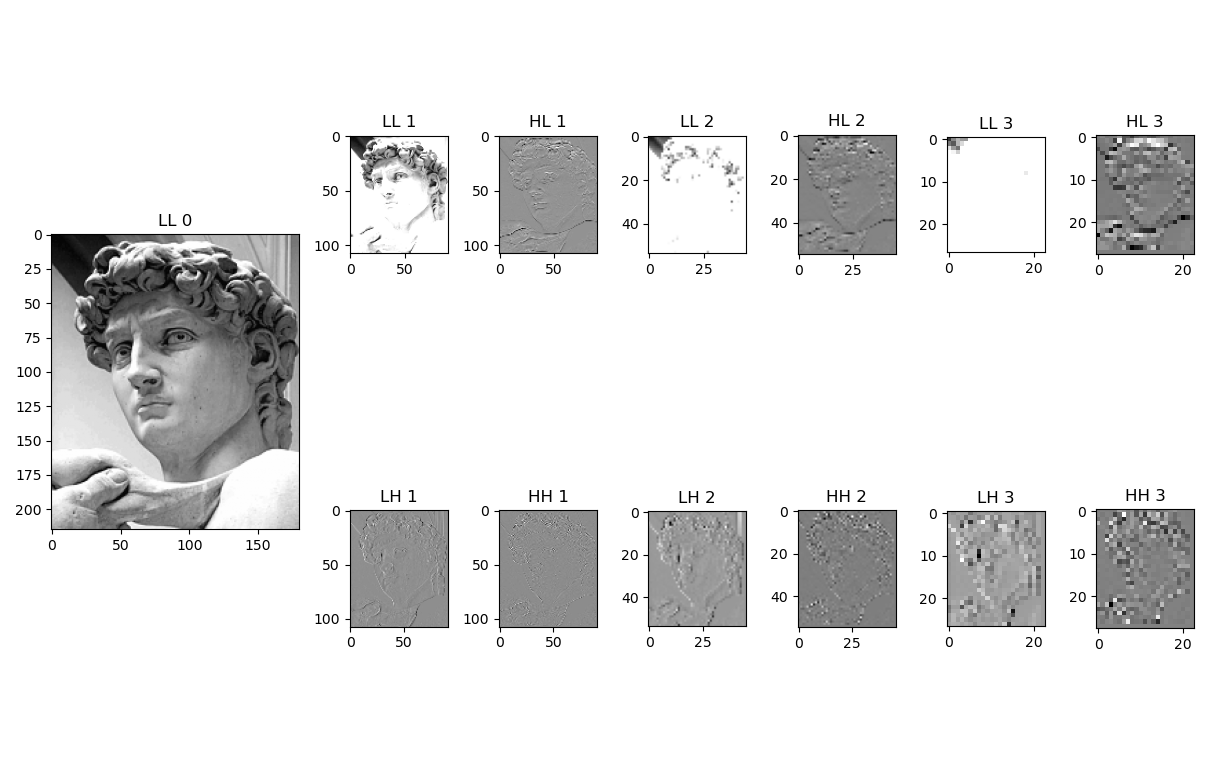
Dekompozycja Fałkowa, jest sposobem rozłożenia sygnału na składowe w celu ułatwienia kompresji danych. Stosowana jest w różnych algorytmach np. JPEG2000. Sama dekompozycja nie kompresuje obrazu, ale ułatwia jego dalszą kompresję. Do rozkładu wykorzystujemy parę filtr Dolnoprzepustowy (L) oraz Górnoprzepustowy (H). Na każdym poziomie filtracji przeprowadzamy filtrację najpierw w jednym kierunku, a następnie w drugim. Każdy z etapów filtracji zapisuje wyniki działania algorytmu na połowie dostępnej do pracy przestrzeni. Następnie przeprowadzamy ponownie filtrację na naszym całym obszarze danych, otrzymując 4 części każdą po innym zestawie filtracji:

• LL - obszar zwierający dane po dwóch filtracjach dolnoprzepustowych
• LH oraz HL - obszary zwierające dane po filtracji dolnoprzepustowej w jednym i górnoprzepustowej w drugim kierunku
• HH - obszar zwierający dane po dwóch filtracjach górnoprzepustowej

Alternatywnie możemy rozmieć te dane jako:

• LL - obraz w niższej rozdzielczości
• LH - wysokie częstotliwości w poziomie
• HL - wysokie częstotliwości w pionie
• HH - wysokie częstotliwości po skosie.

Ponowne składanie obrazu dokonujemy poprzez wykonanie procesu odwrotnego i zsumowanie wszystkich danych ponownie do jednego obrazu.

Przykładowe ustawienia

W ramach tego materiału rozważymy jednowymiarowy przypadek testów. Opiszemy przypadek jednowymiarowy (prawie jak przejście obrazu w jednym kierunku). Na starcie zadeklarujmy sobie kilka informacji potrzebnych do wykonania naszych obliczeń:

• Sygnał wejściowy \(T\)
• Filtr dolnoprzepustowy \(h=[1,1]\)
• Filtr górnoprzepustowy \(g=[1,-1]\)
• Współczynnik skalowania \(\sqrt{\dfrac{1}{2}}\) lub \(1\) lub \(\dfrac{1}{2}\)

Zapamiętujemy i wyliczamy pozostałe współczynniki na podstawie naszych danych wejściowych.

• Długość sygnału \(l\) i połowa długości sygnału \(l2=\dfrac{l}{2}\)
• Długość filtra \(f\)
• Sygnał roboczy \(t\) wydłużony o długość filtra (zeros padding lub mirroring)
• Sygnał po rozkładzie \(y\)

W jaki sposób dokonujemy rozkładu:

for j in range ( l2 ):            
    for k in range ( f ):                
        y [j]    += t [ 2*j + k ] * h [ k ] * s
        y [j+l2] += t [ 2*j + k ] * g [ k ] * s

Jest to przykład jednowymiarowy. W przypadku obrazu trzeba go wpierw rozwinąć o drugą współrzędna i przeprowadzić proces rozkładu w ten sposób wpierw na kolumnach lub wierszach, a następnie na wierszach lub kolumnach (ten drugi wymiar). W celu dokonania funkcji odwrotnej trzeba wykonać te operacje w odwrotnej kolejności, czyli zamiast dodawać wartości, trzeba je podzielić.